Prioriteettijonot ja keko

  1. Johdanto ja määritelmiä
  2. Keon esittäminen taulukkona
  3. Minimikeko vs. maksimikeko
  4. Alkion lisääminen
  5. Suurimman alkion poistaminen
  6. Kekoehdon ylläpito (maksimikeko)
  7. Keon rakentaminen
  8. Kekojärjestäminen
  9. Keon korkeus

6. Kekoehdon ylläpito (maksimikeko)


Algorithm 2 Max-Heapify(A, i)

l ← Left-child-index(i)
r ← Right-child-index(i)
if l < heap-size[A] and A[l] > A[i] then
greatest ← l
else
greatest ← i
end if
if r < heap-size[A] and A[r] > A[greatest] then
greatest ← r
end if
if greatest ≠ i then
Swap(A[i],A[greatest])
Max-Heapify(A, greatest)
end if

Algoritmin idea

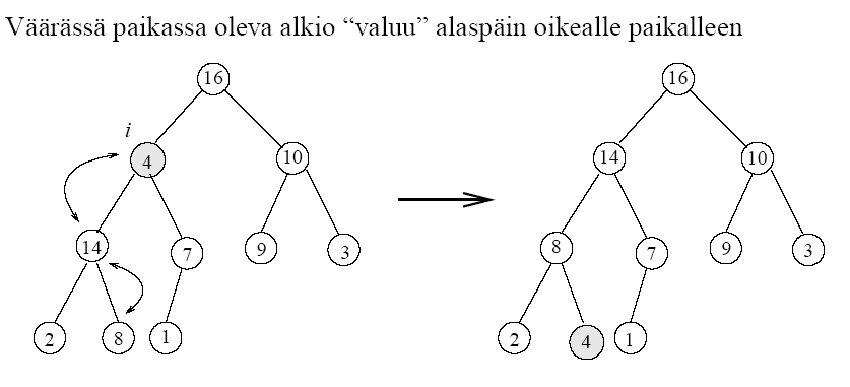
Tässä käsiteltiin maksimikekoja, mutta minimikeon tapauksessa MIN-HEAPIFY(A, i):n toiminta voidaan toteuttaa vastaavantyyppisellä algoritmilla.

Tehtäviä: Suurimman alkion poisto

Maksimikeko on esitetty sekä taulukkona että binääripuuna. Ennen kuin teet tehtävän, tutustu annettuun koodiin ja toteuta operaatiot Left-child-index(i) ja Right-child-index(i) annetulle keolle.

Poista keosta suurin alkio kolme kertaa ja jokaisen poiston jälkeen palauta kekoehto voimaan.

Decrement heapsize -painike pienentää keon kokoa yhdellä. Huomaa, että tehtävässä alkioiden vedä ja pudota -toiminnallisuus vaihtaa lähtö- ja kohdesolmun alkiot keskenään.

Algorithm 3 Heap-Extract-Max(A)

max ← A[0]
A[0] ← A[heap-size[A]-1]
heap-size[A] ← heap-size[A] - 1
Max-Heapify(A, 0)
return max


Algorithm 2 Max-Heapify(A, i)

l ← Left-child-index(i)
r ← Right-child-index(i)
if l < heap-size[A] and A[l] > A[i] then
greatest ← l
else
greatest ← i
end if
if r < heap-size[A] and A[r] > A[greatest] then
greatest ← r
end if
if greatest ≠ i then
Swap(A[i],A[greatest])
Max-Heapify(A, greatest)
end if



Edellinen luku: Suurimman alkion poistaminen Seuraava luku: Keon rakentaminen

This document was last updated 03.11.2011. Please send your comments to Mikko Laakso and Ari Korhonen.