1. Johdanto ja määritelmiä
2. Keon esittäminen taulukkona
3. Minimikeko vs. maksimikeko
4. Alkion lisääminen
5. Suurimman alkion poistaminen
6. Kekoehdon ylläpito (maksimikeko)
7. Keon rakentaminen
8. Kekojärjestäminen
9. Keon korkeus

2. Keon esittäminen taulukkona

• length[A]: taulukon alkioiden lukumäärä (pituus)
• heap-size[A]: taulukkoon A talletetun keon alkioiden lukumäärä
• Huom! heap-size[A] ≤ length[A]
• A[1] on puun juuri, ts. poikkeuksellisesti tyypillisissä toteutuksissa taulukon (keon alkioiden) indeksointi aloitetaan ykkösestä eikä nollasta. Tällöin saatetaan paikkaan A[0] tallettaa keon koko eli A[0] = heap-size[A].

Keko toteutetaan taulukkona, mutta sen toiminta on helpompi hahmottaa, jos se on esitetty binääripuuna. Binääripuuesityksen ja taulukkoesityksen välinen vastaavuus on yksikäsitteinen. Taulukkoesitys saadaan binääripuuesityksestä käymällä alkiot läpi tasojärjestyksessä.

Kuvassa 1 on erään maksimikeon binääripuuesitys, ja sitä vastaava taulukkoesitys.

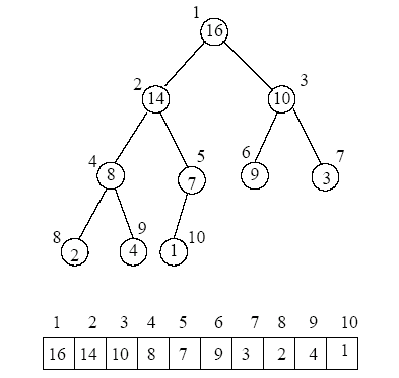
Kuva 1: Maksimikeon [16,14,10,8,7,9,3,2,4,1] binääripuu- ja taulukkoesitys.

2.1 Taulukon käsittelyrutiinit

Tarkastellaan keon i:nnettä solmua, jossa on arvo A[i]

Esimerkki 1: Kuvan 1 solmun i=3 (A[3]=10) isäsolmu on PARENT(3) = 3/2 = 1 (A[1] = 16). Lisäksi sen lapset ovat paikoissa LEFT(3) = 2*3 = 6 ja RIGHT(3) = 2*3 + 1 = 7 (A[6] = 9 ja A[7] = 3, vastaavasti).

This document was last updated 03.11.2011. Please send your comments to Mikko Laakso and Ari Korhonen.