Priority Queue and Binary Heap

1. Introduction
2. Array Representation of Binary Heap
3. MinHeap vs. MaxHeap
4. Insert
5. DeleteMax
6. Preserving the Heap Order Property
7. BuildHeap
8. HeapSort
9. Analysis

2. Array Representation of Binary Heap

• length[A]: the size of the array
• heap-size[A]: the number of items stored into the array A
• Note: heap-size[A] <= length[A]
• The root of the tree is at A[1], i.e., the indexing typically begins at index 1 (not 0). A[0] can be reserved for the variable heap-size[A].

Heap is implemented as an array, but its operations can be grasped more easily by looking at the binary tree representation. The mapping between the array representation and binary tree representation is unambiguous. The array representation can be achieved by traversing the binary tree in level order.

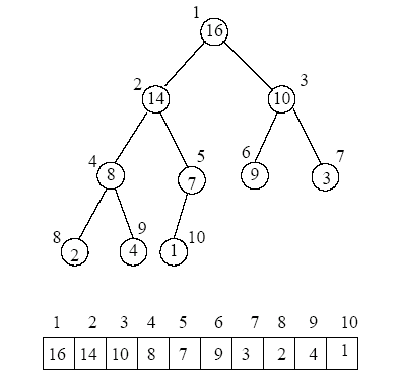
Figure 1: Binary tree and array representation for the MaxHeap containing elements (that has the priorities) [16,14,10,8,7,9,3,2,4,1].

2.1 Routines to access the array

Lets consider the i:th node in a Heap that has the value A[i]

PARENT(i) = i/2	Return the index of the father node
LEFT(i) = 2i	Return the index of the left child
RIGHT(i) = 2i+1	Return the index of the right child

Example 1: In Figure 1, node i=3 (A[3]=10) has father at index PARENT(3) = 3/2 = 1 (A[1] = 16). In addition, its left and right children are at LEFT(3) = 2*3 = 6 and RIGHT(3) = 2*3 + 1 = 7 (A[6] = 9 and A[7] = 3, respectively).

---

Previous Chapter: Introduction Next Chapter: MinHeap vs. MaxHeap

This document was last updated 30.5.2011. Please send your comments to Mikko Laakso, Ari Korhonen, and Ville Karavirta.